Understanding the Feistel Cipher: Design, Mathematics, and Implementation

I wrote a paper a few weeks ago for my Master's program, and I think it would be amazing to transform it into a post for you guys to read. Cryptography is one of the pillars of cybersecurity, so why not dive into one of the most well-known block ciphers out there? Hope you like the reading!

Introduction

The Feistel cipher is a foundational concept in cryptography, forming the structural backbone for many renowned encryption standards, including the Data Encryption Standard (DES). Developed by Horst Feistel, the cipher uniquely combines security, efficiency, and simplicity. This post dives into its historical significance, mathematical structure, design rationale, and practical implementation.

Historical Context

The Feistel cipher was developed out of necessity for a secure, symmetric encryption algorithm that could use the same process for encryption and decryption, simply reversing the order of subkeys. This symmetric approach significantly simplified hardware implementations and reduced complexity. Feistel's design leveraged earlier cryptographic concepts proposed by Claude Shannon, such as confusion and diffusion, which are essential for secure cryptographic systems. DES, built upon the Feistel structure, dominated data encryption standards for decades, paving the way for subsequent advanced standards (Understanding the Feistel Cipher - Best Practices Paper 1 - Gabriel C S Barbosa.)

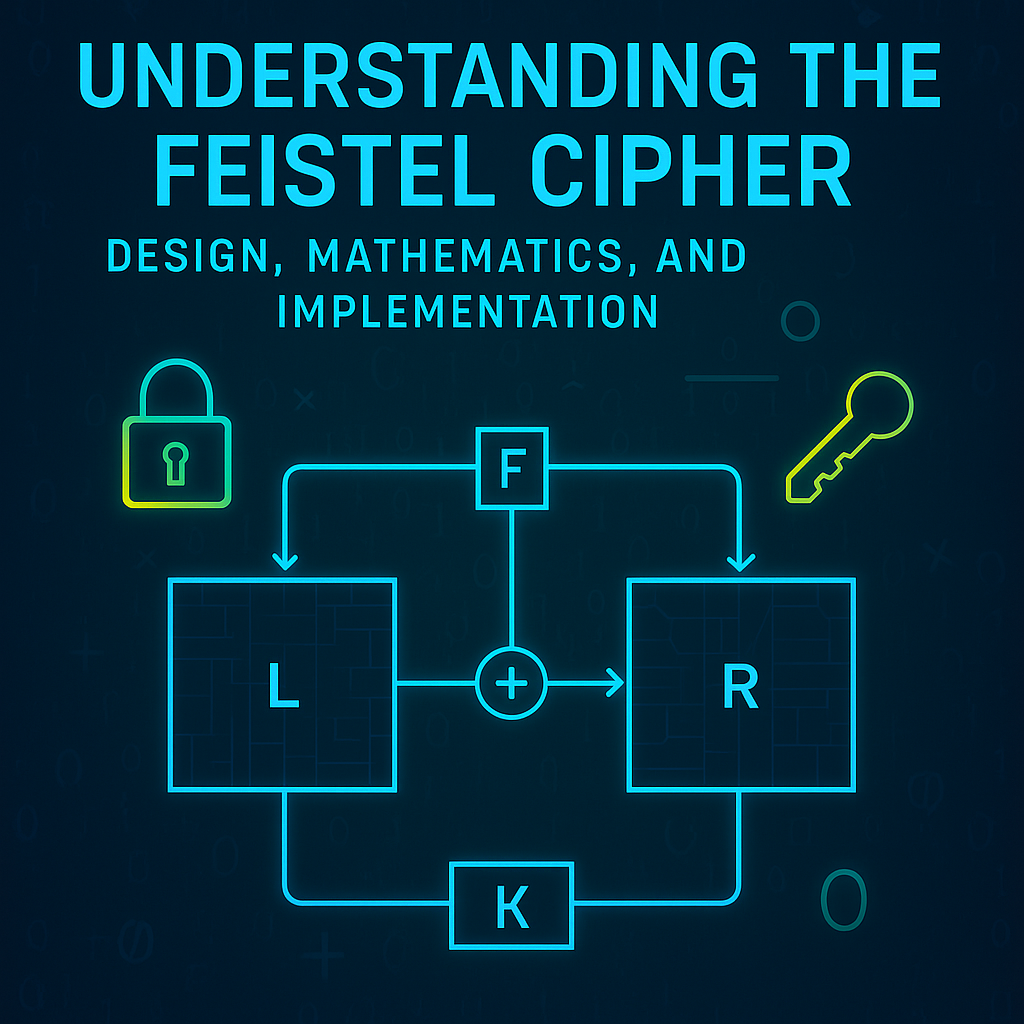
Mathematical Foundations

The Feistel cipher encrypts data by splitting each block into two halves (L0 and R0) and applying multiple rounds of encryption using a round function F. Each round i (where 1≤i≤n) follows:

Li=Ri−1,Ri=Li−1⊕F(Ri−1,Ki)

Where:

• Li, Ri: Left and right halves after round i.
• F: Round function.
• Ki: Subkey for round i.
• ⊕: XOR operation.

Key Design Parameters

• Block Size: Determines security and performance; larger blocks enhance security but may slow processing.
• Key Length: Essential for resisting brute-force attacks; longer keys enhance security.
• Number of Rounds: More rounds improve security, but increase computational demands.
• Round Function (F): Central to security, this function typically uses substitution and permutation to achieve confusion and diffusion.

Python Implementation

Here's a simplified Python example of a 4-round Feistel cipher:

import hashlib

def round_function(data, key):
    return hashlib.sha256((str(data) + str(key)).encode()).digest()[:len(data)]

def feistel_encrypt(plaintext, keys):
    left, right = plaintext[:len(plaintext)//2], plaintext[len(plaintext)//2:]
    for key in keys:
        new_right = bytes(a ^ b for a, b in zip(left, round_function(right, key)))
        left, right = right, new_right
    return left + right

def feistel_decrypt(ciphertext, keys):
    left, right = ciphertext[:len(ciphertext)//2], ciphertext[len(ciphertext)//2:]
    for key in reversed(keys):
        new_left = bytes(a ^ b for a, b in zip(right, round_function(left, key)))
        right, left = left, new_left
    return left + right

# Example Usage
keys = ['key1', 'key2', 'key3', 'key4']
plaintext = b'HelloWorld123456'
ciphertext = feistel_encrypt(plaintext, keys)
decrypted_text = feistel_decrypt(ciphertext, keys)

print('Ciphertext:', ciphertext)
print('Decrypted Text:', decrypted_text)

Security and Performance Trade-offs

The Feistel cipher strikes a balance between security and performance, allowing for iterative enhancements through modularity. Its design is particularly beneficial for environments with constrained resources, as it enables reuse of encryption/decryption circuits. This flexibility enables adjustments and upgrades in response to emerging threats without requiring a redesign of the entire system.

Real-world Applications

Historically, DES utilized the Feistel structure, highlighting its real-world efficacy. Today, encryption standards like AES have evolved using substitution-permutation networks rather than Feistel structures. Yet, Feistel's foundational ideas remain influential and educationally significant.

Conclusion

Studying the Feistel cipher provides valuable insights into symmetric encryption principles, balancing practical utility with theoretical foundations. Understanding Feistel's historical evolution, design flexibility, and mathematical robustness helps cybersecurity professionals design and analyze secure cryptographic systems effectively.

References

• Menezes, A. J., van Oorschot, P. C., & Vanstone, S. A. (1996). Handbook of Applied Cryptography. CRC Press.
• Schneier, B. (1996). Applied Cryptography: Protocols, Algorithms, and Source Code in C (2nd ed.). John Wiley & Sons.
• National Institute of Standards and Technology. (2001). Advanced Encryption Standard (AES).
• Stallings, W. (2017). Cryptography and Network Security: Principles and Practice (7th ed.). Pearson.
• Dilli Hangrai. (2024). Feistel cipher structure—brief study. Medium. Retrieved from https://medium.com/@dillihangrae/fiestel-cipher-structure-brief-study-7934e9b113e4